El problema de Monty Hall
En un concurso se oculta un coche y dos cabras tras tres puertas. El concursante escoge una puerta al azar. A continuación el presentador abre una de las dos puertas restantes conteniendo una cabra. El concursante se queda ahora con solo dos puertas, la que escogió inicialmente y la que queda tras descartar una cabra.
El presentador plantea la siguiente pregunta: «¿Quieres cambiar de puerta o te quedas con la que habías escogido?«
¿Por qué el cerebro se empeña en hacernos seguir una estrategia errónea?
La primera impresión es que cambiar o no cambiar no afecta a las oportunidades, ya que tenemos dos puertas así que la probabilidad debería ser de 1/2 es decir 50% de oportunidades de ganar el coche por lo que la mayoría de gente se aferra a la primera decisión tomada temiendo que el presentador esté tratando de hacerle cambiar para perder, sin embargo esta opción aunque sea la más intuitiva, es incorrecta.
El problema sigue atrayendo la atención de los psicólogos cognitivos.
El comportamiento típico de la mayoría, es decir, no cambiar, puede explicarse por fenómenos conocidos en la literatura psicológica como:
1) El efecto de dotación, en el que la gente tiende a sobrevalorar la probabilidad de ganar de la puerta ya elegida – ya «poseída».
2) El sesgo del status quo, en el que la gente prefiere quedarse con la elección de la puerta que ya ha hecho.
3) Los errores de omisión versus los errores de comisión tienen efecto, en los que, en igualdad de condiciones, la gente prefiere cometer errores por inacción (Quedarse) en lugar de actuar (Cambiar).
hmong.es/wiki/Monty_Hall_problem
La observación cambia la probabilidad.
En principio, cualquier puerta que escojamos tiene una probabilidad de 1/3 de ocultar un coche, por tanto las otras dos puertas restantes forman un conjunto que tiene 2/3 de probabilidad sumada entre las dos.
Cuando al final nos quedamos con solo dos puertas se podría pensar que la probabilidad debería ser de 1/2 pero no lo es ya que partimos de un conocimiento previo el cual ha sido ampliado: Nuestra puerta escogida tiene 1/3 mientras que las otras dos tienen 2/3… si se elimina una de esas puertas entonces queda una sola puerta de ese conjunto con una probabilidad de 2/3 frente a nuestra puerta inicial con probabilidad de 1/3.
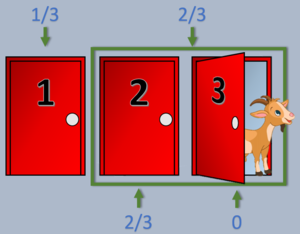
Cuando se abre una puerta del conjunto que tiene 2/3 y se observa que contiene una cabra, ésta puerta adquiere un 0% de probabilidad y automáticamente la puerta restante oculta pasa a sumar todas las probabilidades de ese conjunto de puertas convirtiéndose en una apuesta con 2/3 de probabilidad… ¡El doble que nuestra puerta escogida! por lo que lo más acertado es cambiar la puerta elegida inicialmente.

Exageración.
Mediante una exageración del problema es más fácil visualizar la solución correcta.
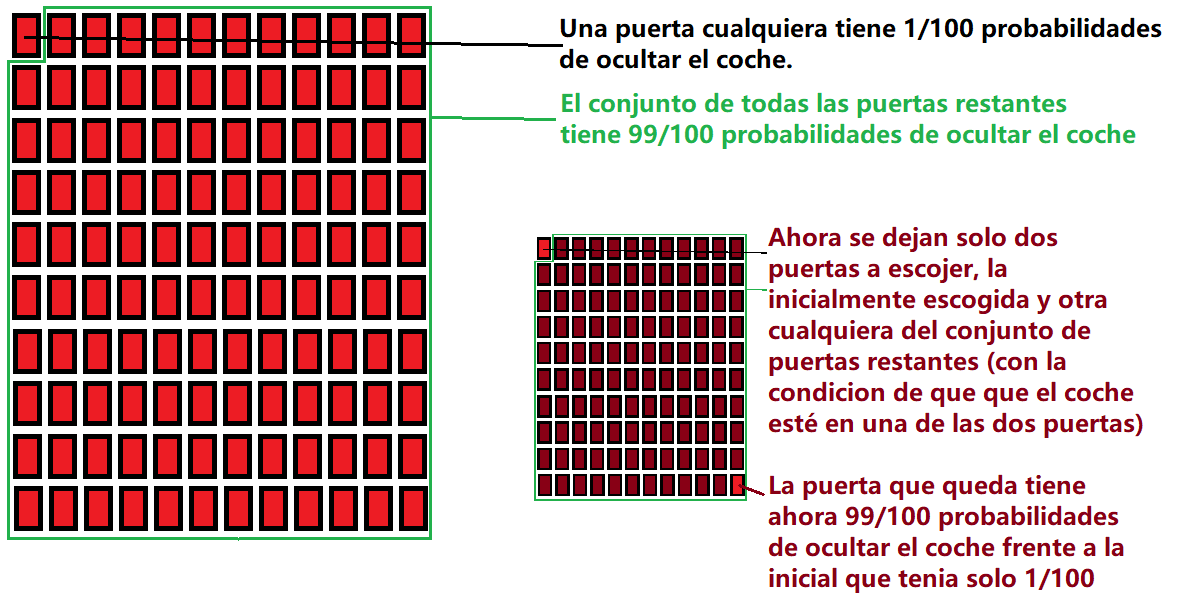
Si en vez de tener 3 puertas tenemos 100, cada puerta tiene una probabilidad de 1/100 y el conjunto de las demás puertas tiene 99/100
Cuando el presentador deja dos puertas a escoger, la inicial y la puerta perteneciente al conjunto de puertas con un 99/100 de probabilidades se entiende que esta última puerta es la que tiene más fácil contener el premio y el cambiar de puerta se vuelve lógico.
Simulación.
Las dos puertas finales no tienen las mismas probabilidades del 50% cada una. Si tienes dudas, puedes jugar y comprobarlo por ti mismo.
Cuantas más veces juegues más se acercará el resultado a la probabilidad estimada: 33% si no cambias 66% si cambias.
Simulación: AQUÍ.
No saben lo que dicen…
Marilyn vos Savant es la persona viva con mayor cociente intelectual. (228)
El 9 de septiembre de 1990, Marilyn vos Savant publicó en su columna la pregunta a este problema y respondió que era mejor seleccionar la segunda puerta, aumentando las probabilidades de ganar el coche de 1/3 a 2/3. A raíz de ello, recibió unas diez mil cartas; la mayoría de los remitentes creía que las probabilidades de ganar el coche –1/2– eran las mismas para las dos puertas. (Wikipedia)
Muchas de las cartas con furibundas críticas eran de matemáticos doctorados.
“Lo arruinaste, ¡Y lo arruinaste en grande! Ya que claramente tienes dificultades para siquiera arañar los conceptos básicos del tema, te explicaré. Luego de que el presentador revela la cabra, tienes una probabilidad entre dos de estar en lo correcto. Cambies o no tu decisión inicial, las probabilidades son las mismas. Hay suficiente analfabetismo matemático en este país, y no necesitamos que la persona con el coeficiente intelectual más alto del mundo lo propague. ¡Vergüenza!
– Scott Smith, Ph.D. Universidad de Florida
Efectivamente, Marilyn vos Savant estaba muy pero que muy lejos de «arañar los conceptos básicos del tema«

![]()
Vota este post:
Total de puntos: 0
